Colloid / Microbe Filtration in Porous Media
Current Funding: NSF/EAR Hydrologic Sciences, Near-Surface Repulsion and Mixing-Limitations: Upscaling of Colloid Transport in Non-Uniform Media under Unfavorable Conditions (co-PI with William Johnson/Utah State and Markus Hilpert/JHU), $159,917 to UC Davis, 2012-2015.
Postdoctoral Associates: Tamir Kamai (now at ARO, Israel), Kirk Nelson (now at USBR, Sacramento, CA).
Students: Andrew Benjamin, Arturo Palomino, Kaveh Zamani (advisee of Prof. Bombardelli).
Collaborators: W. Johnson, USU; Markus Hilpert, JHU; Hervé Tabuteau, Université de Rennes
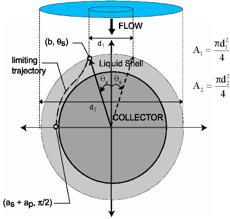
Project Summary: Colloid filtration theory (CFT), which has been widely applied to characterize the transport and deposition behavior of both inorganic and microbial colloids in the natural subsurface, is based in part on a pore-scale analysis of colloid transport in Happel’s sphere-in-cell porous media model. The classical CFT analysis assumes that Brownian motion may be treated independently of the other transport mechanisms, and that colloid entry and exit from near-surface domains is a Poisson process. Recent studies have indicated these assumptions are erroneous. To fix this, we use a fully Lagrangian methodology (2, 6, 8) for treating all classical CFT transport mechanisms simultaneously. In one of our studies (Nelson & Ginn, 2011), numerous simulations were conducted over the relevant ranges of parameter values to provide a basis for a new equation predicting the collector efficiency (rate of contact with porous media surfaces) from the various input parameters. Differences with the classical equation (as well as a more recent one based on a fully Eulerian analysis) are explained in the Lagrangian simulation.
Classical Happel sphere-in-cell. Hydrodynamic energy distributions.
Another challenge is to understand what mechanisms cause long residence times of colloids in porous media under conditions that are unfavorable for colloid attachment (i.e., permanent filtration). We hypothesize that these long near-surface residence times result from incomplete mixing of colloids across the fluid domain, necessitating memory function/multirate or correlated random walk approaches to upscaling. We continue to study colloid fate and transport in lab conditions and with quantitative testing of hypotheses by modeling forthcoming data.
Important papers on the topic:
- Massoudieh A., N. Lu, X. Liang, T. H. Nguyen, T. R. Ginn, Bayesian process-identification in bacteria transport in porous media, J. Contam. Hydrol., 153, 78-91, 2013.
- Nelson K. E., T. R. Ginn, T. Kamai, Comment on “Extending applicability of correlation equations to predict colloidal retention in porous media at low fluid velocity,” Environ Sci Technol., 47(14):8078-9, 2013.
- Nelson, K.E., Ginn, T.R., New collector efficiency equation for colloid filtration in both natural and engineered flow conditions, Water Resour. Res. 47(5) Art. W05543, 2011.
- Massoudieh A. and T. R. Ginn, Modeling colloid-facilitated transport of multi-species contaminants in unsaturated porous media, J Contam. Hydrology, 92(3-4):162-183, 2007.
- Nelson K. E., A. Massoudieh A, T. R. Ginn, E. coli fate and transport in the Happel sphere-in-cell model, Advances in Water Resources 30(6-7): 1492-1504, 2007.
- Ginn T. R., T. Camesano, T. D. Scheibe, K. E. Nelson, T. P. Clement, B. D. Wood, Microbial Transport in the Subsurface, Encyclopedia of Hydrological Sciences, Edited by D. McKnight, John Wiley & Sons Publishing, New York, NY, 2006.
- Nelson, K. E. and T. R. Ginn, Colloid filtration theory and the Happel sphere-in-cell model revisited with direct numerical simulation, Langmuir, 21(6); 2173-2184, DOI: 10.1021/la048404i, 2005.