Inverse Problems
Prior funding: Joint inversion of ground water flow and environmental tracer data for aquifer characterization, 2007-2009, UC Center for Water Resources.
Collaborators: L. Foglia/Tech. Univ. Darmstadt; M. Giudici/Univ. d. Studi di Milano; S. Mehl/CSUChico.
Students: Mohamed Nassar, Tammer Barkouki (graduated, MSCE), Hanieh Haeri (graduated PhD).
Postdoctoral Associates: Laura Foglia (now faculty at Tech. Univ. Darmstadt).
Project Summary: Groundwater management relies on numerical models of flow in aquifers for estimation of effects of management decisions. Aquifers are mostly inaccessible and aside from geophysical techniques that provide good information on short scales and/or for shallow aquifers, hydraulic tomographic techniques provide the primary avenue for enhanced characterization. Hydraulic tomography, the use of multiple pumping tests and observations, also permits characterization of groundwater model parameter values on the scale and template of their definition. One terrific problem stands in the way of aquifer characterization by hydraulic means: the nonuniqueness of the inverse problem (e.g., Giudici et al., 2007). That is, multiple property values may give rise to the observed groundwater pressure data. The parameter values determined may give a good fit to the current groundwater level data, but may not suitably describe the groundwater response to other driving forces, i.e., decreased recharge precipitation per climate change, increased water withdrawals for agricultural purposes, or installation of pump and treat schemes for remediation purposes.
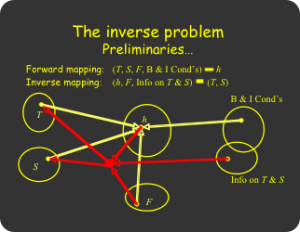
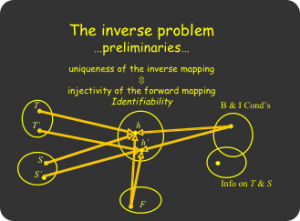
Concepts of existence of inverse solution (left) and uniqueness/identifiability (right).
This research seeks to remedy the situation by bringing to bear previous results on the uniqueness of hydraulic tomography (Ginn and Cushman, 1990; Ginn et al., 1992), including cases where groundwater flow is impacted by density effects (Nassar and Ginn 2014b), to include other valuable data such as inferred groundwater residence time, or age (Ginn et al., 2009). Very recently we have been able to explore how groundwater age, inferred from environmental tracers, can be used in a combined tomographic inverse that finds the aquifer model property values that makes the model fit not only groundwater pressure data but also groundwater inferred age data (Nassar and Ginn, 2014a).
Important Papers in this Topic:
- Nassar, M. and T. R. Ginn, Impact of numerical artifact of the forward model in the inverse solution of density-dependent flow problem, Water Resources Research, 50, doi:10.1002/2013WR014672, 2014b.
- Nassar, M. and T. R. Ginn, Cauchy data requirement of the inverse problem of the mean age equation, Water Resources Research 50(4):3583-3588, 2014a.
- Ginn, T. R., H. Haeri, L. Foglia, and A. Massoudieh, Notes on groundwater age in forward and inverse modeling, Transport in Porous Media,79:117-134, 2009.
- Giudici, M., T. R. Ginn, C. Vassena, H. Haeri, L. Foglia, J.C. Refsgaard, K. Kovar, E. Haarder, E. Nygaard, A critical review of the properties of forward and inverse problems in groundwater hydrology, Proceedings of an International Conference on Calibration and Reliability in Groundwater Modelling: Credibility of Modelling, Copenhagen, Denmark, 9-13 September 2007.
- Ginn, T. R., J. H. Cushman, and M. H. Houck. A Continuous – Time Inverse Operator for Groundwater and Contaminant Transport Modeling I, Deterministic Case, Water Resour. Res., 26:241-252, 1990.
- Ginn, T. R., and J. H. Cushman. A Continuous – Time Inverse Operator for Groundwater and Contaminant Transport Modeling: II, Model Identifiability. Water Resources Research, 28:539-549, 1992.
- Ginn, T. R., and J. H. Cushman, Inverse methods for subsurface flow- a critical review of stochastic techniques, Stoch. Hydrology and Hydraulics 4(1):1-26, 1990.